Hace poco apareció un artículo en El País sobre los
10 momentos más matemáticos de Los Simpsons y ha circulado mucho en redes sociales e internet. Soy un enorme admirador de Los Simpsons y me encanta que la gente esté empezando a quererla por una razón más: su humor ñoño. Uno de los momentos en la lista -los monos en las máquinas de escribir- fue
la excusa para un pequeño artículo que me publicaron en Tzaloa. Sin embargo, me parece que su contraparte de mil años después, Futurama, es mucho más matemática que la familia amarilla. Tiene algo de sentido: el profesor es un profesor, después de todo, Amy es una estudiante de doctorado y los aparatos tecnológicos del futuro requieren alguna explicación más o menos científica. Futurama ha sido llamada la serie más geek de la televisión -incluso si Big Bang Theory pudiera ser más geek, uno espera matemáticas en TBBT pero es sorprendente encontrarlas acá.
Así, como admirador de Los Simpsons, de Futurama y de las matemáticas, estoy encantado de poder compartirles estos chistes matemáticos escondidos a simple vista.
Matemáticos comediantes
Primero, como menciona El País y como muchos saben, tiene muchísimo sentido que ambas series tengan tantas matemáticas. Algunas de las personas más involucradas en la serie tienen títulos de ciencia y matemática:
David X. Cohen, escritor por muchos años de Los Simpsons, fue uno de los creadores de Futurama, más tarde escritor en jefe y productor ejecutivo, estudió Física en Harvard y tiene una maestría en Ciencias de la Computación de UC Berkeley;
Al Jean, escritor y productor ejecutivo de Los Simpsons desde los inicios de la serie, fue también creador de la serie El Crítico, estudió Matemáticas en Harvard;
Jeff Westbrook, escritor de Los Simpsons desde 2004 y recurrente en Futurama también, estudió Matemáticas, Psicología e Historia de la Ciencia en Harvard, para más tarde conseguir su doctorado en Ciencias de la Computación en Princeton;
Ken Keeler ha escrito numerosos episodios de Los Simpsons, es uno de los escritores más prolíficos de Futurama escribiendo algunos de sus episodios más populares, además de haber escrito algunas de las canciones originales de ambas series, estudió Matemáticas en Harvard, se graduó con honores, obtuvo su doctorado y tiene un
número de Erdös de 4, que es bastante elevado.
Esa tiene que ser una de las mesas de escritura más ñoñas de la televisión. El equipo de escritores de Futurama incluía al menos cuatro personas con doctorados: matemáticas, física, química y computación. Futurama es tan ñoña que en uno de los episodios de la nueva temporada de los Simpsons, Simpsorama, donde hay un cross-over entre Los Simpsons y Futurama, el ambiente inmediatamente se vuelve diez veces más ñoño:
Cuando el profesor Frink (Brinco, en español) abre el disco duro de Bender se encuentra cinco ecuaciones, ¿las reconoces? Una de ellas es un teorema muy usado en la Olimpiada, dos de ellas te harán ganar un millón de dólares cada una si logras resolverlas, mientras que las otras dos son sencillamente hermosas.
El artículo de El País menciona el nombre del cine en Springfield,
el Googolplex, haciendo notar que un googol es el número más grande "con nombre". Bueno, el cine en Nueva Nueva York tiene un número un poco más grande
aunque, en realidad, aleph sub cero no es un número sino
un cardinal. Es el tamaño del conjunto de los naturales o de los enteros -que es el mismo.
En un episodio más, Bender se asusta cuando aparece el número 1010011010 escrito con sangre en un espejo. ¿Por qué?
Se trata del número 666 escrito en base dos. En uno de los episodios de la primera temporada, Bender tiene una pesadilla cuando sueña con un 2 que se mezcla entre los 0s y 1s de su código binario. Hay varios más que son los favoritos de muchos:
la ruta 66 (juego de palabras con las homófonas "root" y "route"), las matemáticas
discretas y discretas (en inglés son dos palabras distintas), o
el Studio 57, y una bastante más escondida pero igual de deliciosa:
el archivo P y el archivo NP del profesor.
¿Vamos bien? Apenas estamos comenzando. Vamos a usar Futurama como una excusa para hablar de algo de matemáticas, sobre todo curiosidades que nos permitan explicar algunos chistes; si quieres, puedes seguir las ligas para aprender algo nuevo cada día.
Möbious Dick y Möbius speedway
Hablaremos de dos episodios que juegan con la topología y, específicamente, con la banda de Möbius. El primero de ellos, el episodio
Möbious Dick es un juego de palabras sobre Moby Dick, la famosa novela de Herman Melville, y la
banda de Moebius (Möbious en idioma original, también lo encuentras como Möbius). Por supuesto, como con mucho de lo que hablaremos, conviene que hayas visto el episodio alguna vez.
En el episodio, la tripulación se encuentra con una ballena de la cuarta dimensión que entra a nuestra dimensión a llenar sus pulmones de vacío. Logran darle con un arpón y la tripulación experimenta la cuarta dimensión, que se ve más o menos así:
Además, la ballena tiene tripas en forma de banda de Möbius que, por alguna razón científica, hace que las personas que se han comido no envejezcan. Sin duda, el humor multi y transdimensional se aprecia mejor con los conocimientos de un curso básico de topología. Y hablando de estructuras topológicas, el segundo episodio en esta lista es
2-D Blacktop, un episodio donde el Profesor muestra su amor por la velocidad, pero Leela prefiere la seguridad. Así, juegan una carrera en la pista llamada Möbius Drag Strip, la pista de arrancones de Möbius:

una pista donde ganará el primero en darle "una vuelta alrededor de los dos mismos lados de la pista". De esta manera, los escritores enseñaron espontáneamente la característica más relevante de la famosa banda de Möbius: tiene un único lado, es decir, "derecho" y "revés" son el mismo lado en la banda. Cuando las naves de Farnsworth y Leela chocan de frente -con Fry en medio y Bender adentro- y son enviados a la segunda dimensión, donde el Profesor nos da una nueva lección de topología:
en la segunda dimensión, los seres no pueden comer porque no pueden tener un sistema digestivo pues semejante aparato anatómico los dividiría en dos pedazos separados.
La copiadora Banach-Tarski
En el capítulo
Benderama, el Profesor construye un nuevo invento que llama "Banach-Tarsky Dupla-Shrinker", una máquina que crea dos copias a 60% escala del original agregando un poco de materia, cualquier materia. La máquina se aprovecha de
la paradoja de Banach-Tarsky, que propone básicamente que es posible partir una esfera en pedacitos y luego volver a pegarlos para formar dos esferas idénticas a la original. Los "pedazos" en la paradoja son bastante especiales y se puede con tan pocos pedazos como cinco.
Para entender la matemática -y
si ésta se emplea bien en el episodio- te propongo un par de
lecturas adicionales, si te interesa. En el episodio, el Profesor utiliza la máquina para crear dos copias de su suéter y le pide a Bender que los doble. Bender se rehúsa y, como alternativa, él mismo hace dos copias para que cada uno doble uno de los suéteres. Bender sigue creando copias de sí mismo y emerge un enorme problema
la serie de la masa de los Benders es no-convergente. (Todos parecen darse cuenta de esto excepto Fry, por supuesto.) Esto quiere decir que los Benders eventualmente se acabarían toda la materia de la Tierra creando copias sucesivas de sí mismos.
Números Taxi y el 1729
El número 1729 aparece repetidas veces en Futurama. Por ejemplo, es el número de placa del Nimbus, la nave-estación de guerra de la Tierra comandada por el teniente Zapp Branigan
Es, además, el número de hijo que es Bender
y es uno de los universos que visita Fry en el episodio "Farnsworth Parabox", donde cada universo está encerrado en una caja
¿Y qué es lo que tiene de interesante este número? Bueno, depende de a quién le preguntes. Según el matemático G. H. Hardy, el número no tiene nada de interesante. Una vez visitando a su amigo Srinivasa Ramanujan en la India, quien estaba enfermo, Hardey le comentó que llegó en un taxi con el número 1729 y que le pareció tan exageradamente ridículo que temía fuera una mala señal. Ramanujan le comentó que todo lo contrario, que 1729 era el menor entero que puede expresarse como suma de dos cubos de dos maneras diferentes. Esto es, 1729 = 1^3 + 12^3 = 9^3 + 10^3.
Este número, 1729, se conoce ahora como el número de Hardy-Ramanujan y es el segundo de los taxicab numbers -
números de taxi- en honor a esta anécdota matemática. Se conoce con T(n) al n-ésimo número de taxi, el menor entero que puede expresarse como suma de dos cubos positivos de n maneras distintas. Tenemos que T(1) = 2, T(2) = 1729 y T(3) = 87'539,319. Este número también aparece en Futurama, en un taxi, por supuesto:
En Bender's Big Score -la primera de las películas que salieron directo a DVD luego de la primera cancelación de Futurama- Fry se sube a un taxi cuyo número es, por supuesto, 87539319.
El prisionero de Benda
En las secciones antes que esta, hablamos de cómo un teorema o un concepto matemático servía para crear un chiste recurrente y, a veces, ayudar con la trama de un capítulo. Esto no es distinto de tomar inspiración de cualquier otro elemento de la cultura popular, si acaso más ñoño. En
El Prisionero de Benda, por otro lado, es radicalmente distinto: las matemáticas llegan a salvar un posible hueco en la trama de un capítulo.
En el episodio, el profesor crea una máquina que permite que dos cuerpos cambien de mente. En cuanto lo empiezan a usar, descubren que no es posible que los mismos dos cuerpos vuelvan a intercambiar de mente, para regresar las cosas como estaban. Conforme avanza el episodio, más y más personajes han cambiado de mente mientras el Profesor se pregunta cómo regresarlos. Esto pudo haberse resuelto de varias maneras: como un hueco de trama, donde las cosas simplemente suceden -como la manera en que Batman escapa de prisión y llega a Gótica en un mismo día- o aprovechándose del
Snap Back, un tropo común en televisión mediante el cual las cosas vuelven a ser como siempre cuando empieza el siguiente episodio.
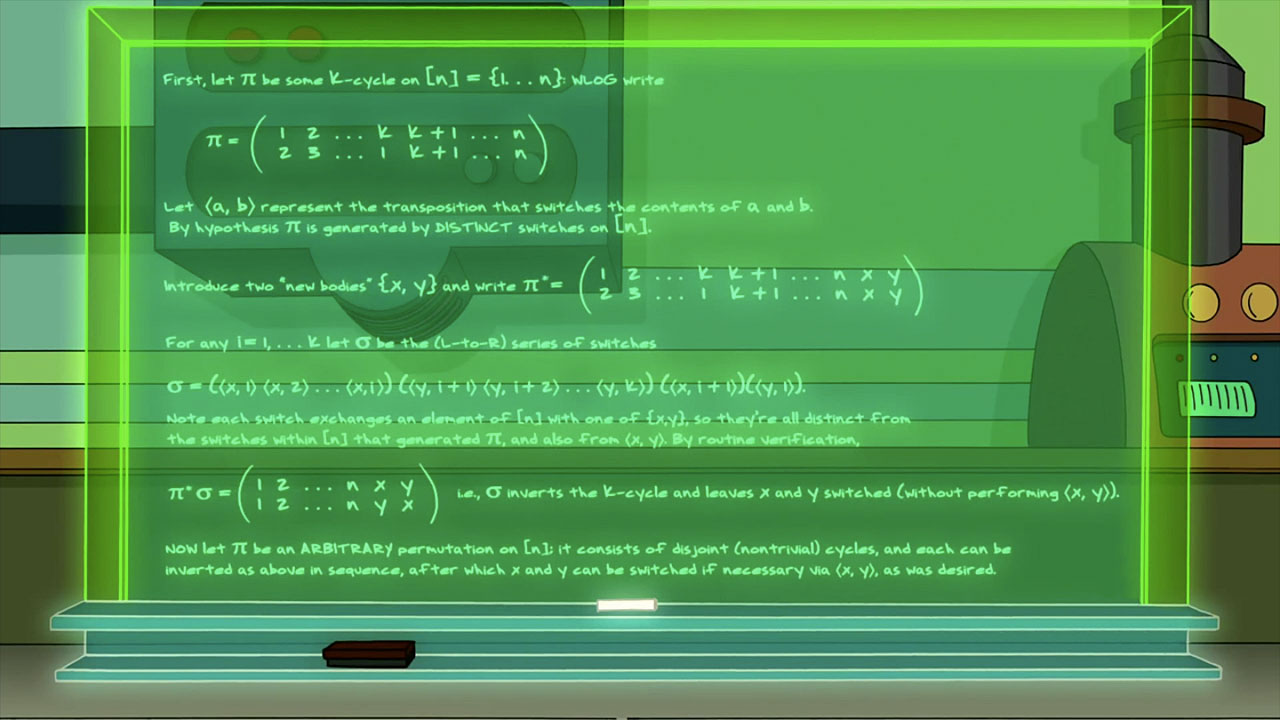
No, los escritores -específicamente Ken Keeler- se pusieron a proponer y demostrar un teorema que les permita volver: demostró que cualquier permutación no-reversible puede volver al estado inicial con la ayuda de dos nuevos elementos. Y la demostración la pusieron ahí, en televisión:
El Teorema, llamado
Teorema de Keeler o
Teorema de Futurama, no es un resultado exageradamente complicado; es un teorema en el sentido en que lo es cualquier resultado matemático, y por eso Ken Keeler siempre ha sentido algo de pena toda la atención que atrajo. Sin embargo, es probablemente el único resultado matemático que ha sido creado específicamente para trabajar en la trama de una serie de televisión.
Hay muchos lugares en internet donde puedes leer más sobre el romance que Los Simpsons y Futurama sostienen con las matemáticas. Te recomiendo
esta entrevista que Wired le hizo a David X. Cohen y Simon Singh, el autor del libro Los Simpsons y sus secretos matemáticos. Si faltaba algo más a tu lista de para qué sirven las matemáticas, sirven para entender los chistes de Los Simpsons y de Futurama.