La cuadratura del círculo y el Teorema Fundamental del Cálculo

Wantzel, Liouville y los números trascendentes

La semana pasada hablamos muchísimo de reglas y compases y lo imposible que resulta resolver tres específicos y muy famosos problemas de la geometría griega usando nada más esas dos herramientas. El problema con la duplicación del cubo, por ejemplo, es que tendríamos que poder construir -usando regla y compás- la raíz cúbica de 2, cosa que es imposible -y por ahí va la demostración de Wantzel. 

No todos los números irracionales son inconstruibles (creo que estoy inventando palabras). Por ejemplo, raíz cuadrada de 2, aunque irracional, se puede construir de manera muy sencilla: construyes un cuadrado de lado 1, trazas su diagonal y ¡pum! construiste un irracional. 

papá...

Sin embargo, un número tan imposible como raíz cúbica de 2 sí se puede construir usando una regla graduada. No es el mismo caso con π, un número mucho más complicado. Es más: la semana pasada pudimos construir con origami un número que no es construible con regla y compás; el truco fue usar el doblado de papel para poder resolver un polinomio cúbico. No es el mismo caso con π, un número mucho más complicado. Para entender qué tan complicado, tenemos que hablar de Liouville y sus números, es decir, los números de Liouville.

El francés Joseph Liouville, construyó un número como sigue: cada dígito después del punto decimal es 1 si está a exactamente n! posiciones después del punto, para algún n, y es 0 en caso contrario. El número de Liouville -en singular- se ve más o menos así: 0.11000100000000000000000100..., y continúa infinitamente. Liouville no tardó mucho en demostrar que se trata de un número irracional, pero hizo todavía más que eso: demostró que su número no podía ser la raíz de un polinomio con coeficientes enteros. Los números que sí son raíces de algún polinomio con coeficientes enteros se llaman algebraicos; los que no, se llaman trascendentes. Los números de Liouville son un tipo especial de números trascendentes: aquellos que se pueden aproximar muy bien con un racional. 

no confundir con la otra trascendencia

No podemos aquí entrar a detalles, pero resulta que π no solo es irracional, además es trascendente. Esa parte la demostró Ferdinand Lindemann en 1882. De hecho, algunos números famosos son trascendentes, como e; también los logaritmos naturales de reales positivos -excepto potencias de 10- y los valores de funciones trigonométricas —salvo algunos casos. En realidad, hay muchos, muchísimos más números trascedentes que algebraicos, en el mismo sentido en que hay infinitamente más números irracionales que racionales. Hay números de los que ni siquiera sabemos si son algebraicos o no, como la constante de Euler, de la que ni siquiera sabemos si es racional o no. En la sección final te dejamos enlaces a demostraciones tanto de la trascendencia como de la irracionalidad de π. 

Con π un número trascendente, podemos darle carpetazo al problema de la cuadratura del círculo con regla y compás, con origami y con métodos similares. Sin embargo, los problemas de cuadratura no se reducen únicamente al del círculo e intrigaron a matemáticos tan famosos como Isaac Newton y Gottfried Leibniz, por si te imaginas para dónde va esto. 

Ferdinand de Lindemann y su estilo trascendente

La cuadratura y los fluxones

Aunque para mucha gente parece que la expresión "buscar la cuadratura del círculo" equivale a la expresión "buscarle tres pies al gato", que lo entiendo porque nunca me ha quedado claro qué quiere decir eso del gato. En realidad, la cuadratura de una curva se refiere a encontrar un cuadrado —o, en todo caso, un rectángulo— cuya área sea la misma que la de la curva. La cuadratura del círculo es un problema que pide construir un cuadrado cuya área sea la misma que la del círculo. El problema es imposible de resolver usando nada más regla y compás pero construir un cuadrado con la misma área no es difícil. Si estos problemas te suenan familiares, quizás se deba a que has llevado un curso de Cálculo Integral, donde nos dedicamos a calcular el área entre el eje y una curva. 

pff... eso fue fácil

Son cuatro tipos de problemas los que dieron origen al Cálculo: (1) dada la fórmula para distancia como función de tiempo, encontrar velocidad y aceleración instantánea, y al revés; (2) construir una tangente a una curva por un punto dado; (3) encontrar valores máximos y mínimos a una función; (4) encontrar área y volumen acotado por curvas y superficies. Los problemas de tipo (2) se llaman "problemas de tangentes" y los problemas de tipo (4) se llaman "problemas de cuadraturas". Estos dos tipos de problemas fueron planteados originalmente por los griegos. 

Encontrar las cuadraturas de ciertas figuras no es demasiado. Por ejemplo, piensa que las fórmulas de área que conocemos están todas en función de la del triángulo, que a su vez está en función de un rectángulo. El griego Hipócrates de Quíos construyó cierto tipo de curvas cuadrables que llamó lúnulas. Después de él, Euler encontró otro tipo de lúnulas y más o menos hasta ahí llegamos. 

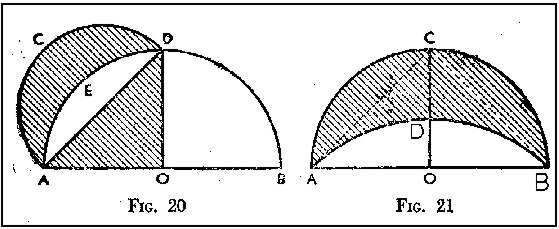lú-nu-la

El detalle es que tanto Isaac Newton (1642-1727) como Gottfried Leibniz (1646-1716) vivieron antes de que se demostrara que el problema no tenía solución -de nuevo, con métodos de regla y compás- por lo que dedicarse a él no sonaba muy descabellado. Resolver este problema hoy en día sencillamente nos lleva a pensar en el Cálculo Integral. De manera parecida, el problema de la tangente pensaríamos inmediatamente en usar Cálculo Diferencial. De esto aprendemos varias cosas: (1) esos griegos estaban en todo, (2) preguntas muy sencillas planteadas desde la curiosidad inocente pueden necesitar siglos para contestar y llevar a la creación de herramientas muy sofisticadas y maravillosas. Ellos dos —como muchas de las personas que intentaron resolver estos problemas— encontraron que sus soluciones estaban más o menos relacionadas. 

Nos vamos a adentrar de lleno en el mundo del Cálculo. 

En la obra Lectiones Geometricae de Isaac Barrow (1630–1677) —por cierto, maestro de Isaac Newton— encontramos un primer intento de formalizar —con la formalidad matemática de la época, por supuesto— estas intuiciones en lo que conocemos hoy como la versión geométrica del Teorema Fundamental del Cálculo. El trabajo que Barrow y sus colegas hacían con respecto al cálculo de tangentes seguía un método propuesto por Fermat y que, en principio, parece una alternativa muy obvia aunque no inmediatamente más sencilla: para calcular la tangente que pasa por un punto, basta con conocer otro punto que pertenezca a la tangente. Este método —conocido como método de la subtangente y que es muy querido y defendido por los socioespistemólogos— consiste en calcular el punto de intersección de la tangente con el eje x buscando cierta semejanza de triángulos; la subtangente es el segmento de recta que va desde la proyección del punto de interés sobre el eje x hasta la intersección con el eje x de la tangente a la curva por dicho punto de interés.

Una de las sorpresas más agradables al iniciar un curso de Cálculo Integral es aprender el Teorema Fundamental del Cálculo que relaciona el proceso de la integración como un proceso inverso al de derivación. Esa idea no es posterior a su creación; es decir, no es que se hayan inventado los Cálculos y luego se haya descubierto que están relacionados, es una idea está en el origen mismo, precisamente en la relación de la cuadratura y la tangente. No sé ustedes, pero eso lo hace todavía más maravilloso. Barrow resuelve el problema de trazar una tangente a una curva cuando ésta es la cuadratura de otra curva, relacionando sus cuadraturas. La demostración de Barrow se conoce hoy como demostración geométrica del Teorema Fundamental del Cálculo. 

Lo que hace Leibniz es reducir el problema de cuadraturas a una versión inversa del problema de las tangentes, algo bastante parecido a lo que hizo Barrows: “Demostraré ahora que el problema general de cuadraturas puede ser reducido al de encontrar una línea que tiene una ley de tangencia dada”. Leibniz se apoya del triángulo característico, un triángulo rectángulo cuyos lados eran paralelos a los ejes y uno de sus vértices coincidía con el punto dado sobre la curva. Los lados del triángulo paralelos a los ejes tenían dimensiones dx y dy, respectivamente, pues eran las distancias del punto dado a otro vértice del triángulo —el que estaría sobre la tangente. Del hecho de que Leibniz buscara una semejanza con este triángulo se desprende nuestra notación actual de dy/dx para la derivada: a diferencia de Barrow, no busca el punto que cumpla una igualdad de área sino el que satisface una relación de proporcionalidad. 

se hace pequeño, pequeño, pequeñiiito...

Vemos en Leibniz que la pendiente de la línea tangente de una curva y el área de otra curva dada están en estrecha relación. Esta es la relación que existe entre el problema de la tangente y el de la cuadratura, relación que se extiende a la derivada y la integral. 

El trabajo de Leibniz y el de Barrow en atacar los problemas de cuadratura y derivada tiene fuertes similitudes. Curiosamente, el de Newton —alumno de Barrow—, guarda menos semejanzas. Newton estaba interesado en calcular el área debajo de curvas exponenciales porque esas curvas —fluentes— guardaban estrecha relación con las razones de cambio —fluxiones— de otras curvas. En su trabajo, Newton demuestra —o propone, al menos— una regla para calcular el área de dichas curvas exponenciales que demuestran la estrecha relación entre problemas de cuadratura y tangente: para calcular la cuadratura de una fluente, bastaría con encontrar una curva cuya flexión es, precisamente, la fluente. 

flu-xio-nes

Encontramos en los trabajos de Barrow, Leibniz y Newton —trabajos fundadores del Cálculo— no solo posibles soluciones a los problemas de tangente y cuadratura sino una estrecha relación entre las soluciones a ambos problemas: parece, pues, que la solución de la cuadratura puede reducirse a tangentes y la solución de la tangente a cuadraturas. Recordemos que en tiempos de Newton y Leibniz no existía el concepto de límite. El trabajo de Leibniz se apoya en los infinitesimales —de manera burda, números lo suficientemente pequeños como para ser eliminados de los cálculos— y el de Newton en el concepto de fluxión —entendido hoy como razón de cambio. El concepto de límite está en el corazón de nuestras definiciones de integral y derivada por lo que la definición que ellos tenían no era, en este sentido, independiente. 

Así, en el nacimiento del Cálculo, los conceptos de integración y derivación están estrechamente ligados al punto de entender uno como el proceso inverso del otro: el mismísimo Leonhard Euler (1707-1783), por ejemplo, define el cálculo integral como “el método de encontrar, a partir de un diferencial dado, la cantidad misma; y la operación que produce esto, es generalmente llamado integración”. Es, pues, hasta Cauchy (1789-1857) y la llegada del concepto de límite que podemos definir a la derivada y la integral de manera independiente. Sin embargo, el propio Cauchy se dio a la tarea de demostrar la relación formulando ambas partes del Teorema Fundamental del Cálculo, si bien él nunca le da semejante adjetivo. 

La pelea sobre la paternidad del Cálculo se ha nutrido mucho tiempo de la diferencia entre europeos continentales y europeos de la isla, y le ha dado tintes de batalla épica a la relación entre Liebniz y Newton. Si hubieran resuelto sus diferencias a tiempo, quizás también hubieran podido ser los padres del heavy metal de larga cabellera. 

Para hacer en casa:

Puedes... pues, tú sabes, aprender Cálculo. Nos hemos saltado aquí parte del desarrollo didáctico natural de la enseñanza del Cálculo Integral que es aprender sumas de Riemann. Cálculo Integral normalmente se ve después del Diferencial, que lo empuja hasta sexto semestre de preparatoria. Así, te puedes adelantar a lo que vas a ver echándole un ojo aunque sea a la Wikipedia. 

Barbas 2, Cabelleras 2

Para saber más:

Nos saltamos todas las demostraciones y te las dejamos aquí agrupadas de manera bonita: 

Eugenio P. Balanzario, del Instituto de Matemáticas UNAM-Morelia, tiene estas notas sobre números irracionales y trascendentes donde puedes aprender mucho más de lo que necesitas. Ahí están las demostraciones prometidas motivadas con ejercicios previos. 

Para ver un poco más sencillo —no demasiado— que π es un número irracional, puedes visitar a nuestros amigos los Gaussianos, o bien, confía en la Wikipedia como hacemos los millenials. 

Puedes seguir paso a paso, casi directamente del latín original, el planteamiento y demostración geométrica del Teorema Fundamental del Cálculo de Isaac Barrow en esta entrada del blog Divergiendo. 

Juan Carlos Ponce Campuzano hizo su tesis en estos asuntos del origen del Cálculo, por lo que sabe muy bien de lo que escribe. Aunque hay varias publicaciones suyas en internet, te pasamos ésta que liga directo a su página de scribd y que ofrece distintas demostraciones del TFC, incluyendo la de Barrow.