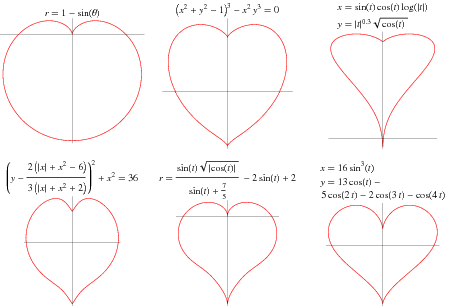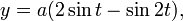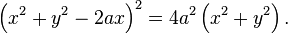Cada año, durante las dos semanas entre el Super Bowl y el día de la Bandera en México, la gente decide tomarse un tiempo para expresar el amor que sienten por aquellas personas más cercanas como la pareja o los amigos. Es natural que la gente que siente un especial cariño por las matemáticas encuentre la manera de expresar su amor de alguna manera matemática.
Es una muy buena alternativa, pero las ideas son escasas a veces. Podrías regalar un pendiente con el símbolo matemático del amor, <3, que es ya tan universalmente difundido y adoptado como emoji que de matemático ya no tiene tanto. Podrías buscar en la expansión decimal de Pi para encontrar la secuencia de dígitos que corresponde a tu aniversario diciendo que era destino o algo así (aunque sería mejor para todos evitar lo más posible los mitos del amor romántico; además, probabilísticamente, es casi seguro que encuentres cualquier secuencia, de modo que sería mentira).
Sea como sea, hoy hablaremos de las cardioides y hemos incluido un tutorial por si quieres regalar una. Sin embargo, me siento legalmente obligado a pedirte que tengas cuidado con lo que regales este día.
Existen numerosas maneras de tratar de introducir tu amor por las matemáticas en la manera en que expresas tu amor por los más cercanos a ti, quizás sobre todo tu pareja. puedes intentar replicar esta escena de una película que no conozco, sobre un supuesto problema y su inesperada solución:
o podrías escribir una desigualdad y pedir que despejen para i esperando que lleguen a la solución de la manera en que es importante que quede expresada para que tenga sentido:
que, por cierto, si te apuras, puedes pedir una versión bordada desde esta tienda de Etsy. Sin embargo, nada muestra tu amor que una cardioide.
¿Qué es una cardioide y por qué?
Existen varias maneras de definir una cardioide; vamos a revisar cinco definiciones distintas. La primera definición espirógrafa es como un caso particular de las epicicloides. Las siguientes dos la describen como una curva paramétrica, las otras dos como envolvente de distintas familias.
Epicicloides, hipocicloides,
Hay muchas curvas que se pueden encontrar viendo cómo se comportan puntos fijos en una circunferencia conforme éstas giran. Por ejemplo: la cicloide, que es el rastro -o lugar geométrico- que un punto fijo sobre una circunferencia deja conforme ésta se mueve -sin deslizarse- sobre una recta.
Si alguna vez tuviste un espirógrafo, entonces perteneces a una generación que se podía entretener de maneras mucho más simples. Además -y mucho más relevante aquí- conoces bien las curvas epicicloides y las hipocicloides: curvas que se obtienen al estudiar puntos fijos en circunferencias cuando giran sobre una circunferencia fija -normalmente de mayor radio-. Cuando la circunferencia gira en el exterior de la circunferencia fija, la curva es una epicicloide; cuando gira por adentro, se llama hipocicloide.
De estas familias de curvas, únicamente nos interesa la cardioide, que es un caso particular de la epicicloide: cuando el círculo que gira y el círculo fijo tienen el mismo radio.
Cuando la razón entre los radios cambia, se obtienen algunas otras figuras bonitas. Por ejemplo, si el radio de la circunferencia exterior es la mitad, entonces es una nefroide; si es la tercera parte, entonces es una trifoide; y así sucesivamente, hasta que se cruzan y se forman florecitas.
Algo similar pasa con las hipocicloides, de las que te mostramos algunos casos:
En todas estas figuras, k es la razón del radio de la circunferencia mayor -fija- con respecto al radio de la circunferencia menor -la que gira-. Podemos expresar k = R/r. Así que si tienes por ahí tu espirógrafo viejo guardado, es momento de desempolvarlo y usarlo para enseñar matemáticas.
Ecuaciones paramétricas
Una ecuación paramétrica es aquella que, vaya, depende de un parámetro. Este parámetro recorre valores reales en cierto intervalo. Por ejemplo, para describir una parábola, podemos escribir la ecuación paramétrica c(t) = (t, t^2); podemos escribir la ecuación paramétrica de un círculo como c(t) = (cos t, sin t), para valores de t entre 0 y 360.
En el caso de la cardioide, la ecuación paramétrica está en términos de senos y cosenos. Escribimos la ecuación paramétrica c(t) = (x(t), y(t)) de la siguiente manera:
donde a es el radio de ambas circunferencias y t es el parámetro.
Estas ecuaciones se pueden reescribir de manera muy sencilla de manera polar, donde el parámetro es el ángulo theta, de la siguiente manera:
Si juegas con los valores de seno y coseno, suponiendo que la circunferencia tiene diámetro 1, entonces puedes crear la cardioide "unitaria", que puede girar para hacer los riñones, el corazón y las pompis unitarias:
Finalmente, de manera no-paramétrica y en coordenadas cartesianas, la ecuación de una cardioide se puede escribir de la siguiente manera:
Envolvente
Finalmente, vamos a ver dos definiciones de la cardioide como distintas envolventes. Una envolvente es una curva que, vaya, envuelve una familia de curvas (que pueden ser circunferencias, rectas, parábolas, exponenciales,...) de modo que cada punto de la curva envolvente es tangente a un miembro de la familia de curvas que envuelve. Vamos a verlo con dibujitos:
Por ejemplo, en un ejercicio típico en materias de Geometría Analítica o Cálculo -o a veces de Dibujo Técnico o Artísticas- cuando tu profe no sabe qué ponerte, es unir ciertos puntos correspondientes para crear una parábola:
Es importante ver que la parábola NO está dibujada, solo es mucho más clara mientras más rectas dibujes. Esta idea es sumamente importante en Cálculo Diferencial: no conocemos la parábola, pero si conocemos todas las rectas tangentes a ésta, básicamente conocemos la parábola. Como podemos entender el valor puntual de la derivada como la pendiente de la recta tangente en ese mismo punto, podemos conocer perfectamente una curva si conocemos la derivada.
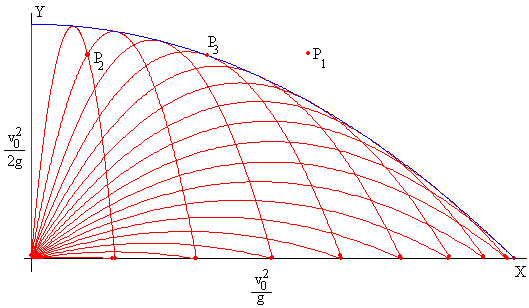
Hay otras figuras que aparecen como envolventes, por ejemplo en la física. Existe una parábola llamada "parábola de seguridad" que es la envolvente de una familia de parábolas que pasa por su máximo alcance y máxima altura, de modo que en un tiro parabólico estás completamente a salvo si estás fuera de esta parábola:
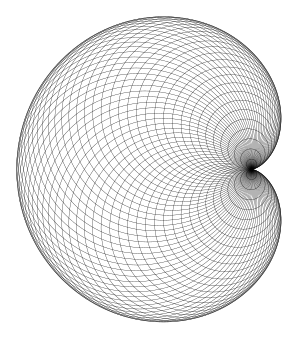
La cardioide aparece aunque no esté realmente dibujada, y el patrón de dibujo se ve muy bonito. La regla, como dijimos, es trazar una circunferencia y elegir un punto en ésta. Luego, para algunos puntos sobre esa circunferencia fija, tomarlos como centros y trazar los círculos que pasan por el punto fijo. A ver si esto es más claro:
Por supuesto, mientras más circunferencias traces, más clara es la cardioide. En esta página, puedes jugar con un applet que te permite ver cómo es más y más clara la cardioide conforme aumenta la cantidad de circunferencias trazadas.
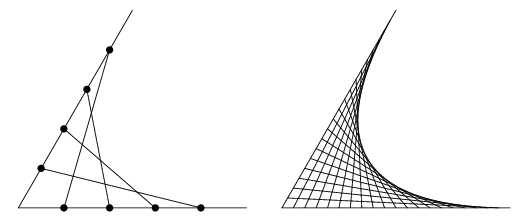
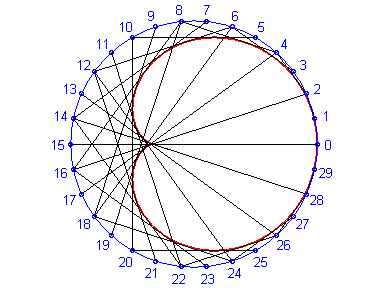
El punto central de esta entrada -que casi siempre terminan siendo los puntos finales- era la definición de la cardioide como una envolvente de rectas. La figura completa se ve más o menos así:
De nuevo, mientras más rectas traces, más clara es la curva. En la figura anterior, la cardioide sí fue remarcada con rojo. La instrucción es realmente sencilla: en un círculo, trazas un n-ágono para un n más o menos grande, es decir, marcas alguna cantidad grande -por ejemplo 72- de puntos equidistantes en el círculo. Luego, los enumeras. El resto es fácil, traza una recta que una cada punto con su doble: el 1 con el 2, el 2 con el 4, el 3 con el 6, el 4 con el 8, y así sucesivamente. El 36 va con el 72 y, si solo trazaste 72 puntos, el 37 iría con el 2, el 38 con el 4, el 39 con el 6, y así de nuevo. (Esto es, el doble módulo 72, o módulo la cantidad de puntitos que hayas puesto.)
Si en lugar de unir cada punto con su doble lo haces con su triple, construyes una nefroide. Si es con su cuádruple, construyes una trifoide -o sea, una figura con tres bolitas-. Y así se sigue.
Para hacer en casa
La cosa divertida e interesante con las envolventes es que puedes hacerlas con lápiz y papel. Ya te pasamos las reglas para hacer las cardioides, de modo que lo único que te hace falta es una regla y un círculo graduado. Para ahorrarte ese trabajo, puedes descargar patrones circulares desde aquí. Esto puede mantener a un grupo de jóvenes entretenidos por un buen rato, seguro funciona muy bien con niños y niñas.
Puedes usar plumas de colores o colorear los espacios que quedan para crear diseños y patrones muy bonitos. Además, con algo de habilidad manual, se puede convertir en tu regalo de San Valentín. Necesitas lo siguiente:
- Un pedazo de madera, de preferencia cuadrado. (Vas a trazar un círculo que cabe bien en un espacio cuadrado, pero si es rectangular te sobra espacio para lo que quieras.) Nosotros usamos un pedazo de 61x61cm de triplay que es enorme -y una madera medio de mala calidad-. Lo importante es que sea gruesa para aguantar los clavitos.
- Muchos clavos y un martillo. Con 72 -que son más o menos fáciles de colocar- la figura se ve bastante bien. La cardioide que mostramos tiene 78 clavos; el otro diseño tiene 172.
- Estambre y tijeras. Compramos una de esas bolas de estambre y nos sobró muchísimo.
- Lo necesario para trazar tu 72-ágono: compás, lápiz, goma, regla.
El primer paso es trazar tu 72-ágono. Una manera sencilla es trazar el círculo y luego usar tu compás para marcar divisiones según la cantidad de grados (en este caso 5) en que quieres marcar. Recuerda que debes enumerar los vértices.
El siguiente paso es clavar tus clavitos. Esto toma un buen rato y, dependiendo de tu habilidad manual y coordinación mano-ojo, quizás quieras pedir ayuda.
El resto es sencillo: amarra un extremo del estambre en el 1 y ve uniendo los puntos con su doble. Para no cortar el estambre -que tomaría años- pasa por atrás de los clavitos. Por ejemplo, puedes hacer el siguiente ciclo: 1, 2, 4, 8, 16, 32, 64, 56, 40, 8. Ahora, puedes pasar por atrás de los clavitos para irte hacia el 7 o hacia el 9 -el que quieras- y volver a empezar. De esta manera no tienes que estar cortando y amarrando el estambre.
La figura terminada debe quedarte más o menos así:
(Aquí tenemos pensado subir un video sobre cómo hacerlo con madera, clavos y estambre. Si no está aquí el video, es que no lo hemos subido.)
Además, si eres una persona cursi como yo, el estambre sirve perfectamente como un "tendedero" de modo que puedes colocar fotografías y usarlo como regalo del corazón:
Puedes hacer que tu cardioide parezca más un corazón estándar si le agregas medio patrón circular. En este sitio te dicen cómo de manera sencilla. La figura terminada terminaría así:
(Al menos, así se ve con estambre rojo en una madera de triplay de 61x61 con 172 clavitos. Puedes jugar con estambres de distintos colores o puedes pintar tu madera para hacer contrastes. No tiene que ser algo así de grande para que se vea bonito -ya con 72 clavitos se ve perfecto e incluso con 30-60 funciona bien- pero esa es más o menos la clase de persona que soy yo.)